How Computer Works – Part 2
Tác giả: Vũ Tùng Minh, Học viên khóa 2020-2023
Tính toán nhị phân (Binary addition theory)
Hãy bắt đầu bằng phép tính đơn giản nhất, phép cộng. Một phép toán mà trẻ con mẫu giáo cũng làm được thì có gì phải tìm hiểu nhỉ? Không đơn giản như vậy, ta đã biết máy tính không sử dụng hệ thập phân (decimal) thường thấy mà sử dụng hệ nhị phân (binary), vậy nên khó khăn ở đây chính là làm sao để hiểu và tính toán với các con số trong hệ nhị phân.
Cùng xét qua ví dụ sau:

Ta có 100011 + 111. Thực hiện tương tự các bước như khi làm phép cộng trong hệ thập phân.
Lần lượt từ phải sang trái, ta có 1 + 1 = 2 tức trong hệ nhị phân sẽ là 10. Vậy nên ta viết số 0 vào kết quả và nhớ 1 đơn vị vào cột tiếp theo.
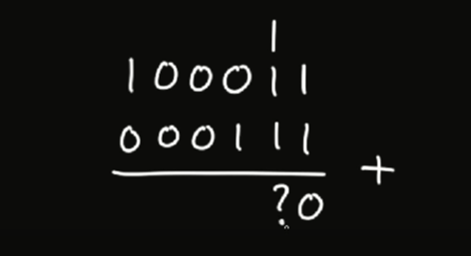
Câu hỏi ở đây là kết quả của phép tính tiếp theo sẽ là gì?
Dễ thấy, 1 + 1 + 1 = 3, nghĩa là trong hệ nhị phân sẽ là 11.
Ta viết 1 vào kết quả và nhớ 1 vào phép cộng tiếp theo.
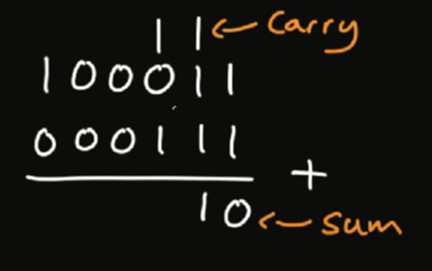
Wao, khá là đơn giản. Bằng vào tư duy của các bạn, hãy hoàn thành nốt phép tính này xem kết quả cuối cùng có đúng không nhé?
Tôi sẽ để kết quả ở bên dưới, đừng vội lướt xuống.
Cuối cùng, ta có 100011 + 111 = 101010 tương đương với 35 + 7 = 42 .

Xây dựng mạch logic ADDER
Xét vấn đề theo góc nhìn tổng quát, ta dễ dàng nhận ra để cộng được 2 số nhị phân, ta cần phải cộng dồn từng bit lần lượt từ phải sang trái, vậy bài toán cơ sở ở đây là “làm sao để cộng 2 bit nhị phân, 3 bit nhị phân với nhau?”. Dễ mà, đối với cộng 2 bit, ta có thể xây dựng ra một bảng chân lý như sau:
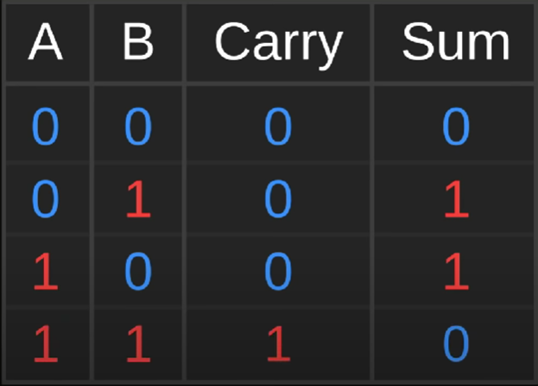
Trong đó, A và B là hai bit đầu vào. Đầu ra ta có Carry là bit nhớ, tức là phần dư của phép tính cộng, Sum là kết quả cuối cùng. Ta hiểu bảng chân lý trên như sau:
| 0 + 0 = 0 (nhớ 0) |
| 0 + 1 = 1 (nhớ 0) |
| 1 + 0 = 1 (nhớ 0) |
| 1 + 1 = 1 (nhớ 1) |
Dễ thấy kết quả của Carry tương đương với kết quả của mạch AND, vậy nên ta dùng luôn nó vào trong mạch. Ngược lại, kết quả của Sum có vẻ khó nhằng, nó vừa giống mạch OR nhưng lại giống mạch NAND. Thực ra mạch này có tên gọi riêng của nó, ta gọi nó là XOR, bảng chân lý của nó cũng giống hệt kết quả của Sum nên ta không nhắc lại ở đây. Hãy bắt đầu bằng việc xây dựng mạch XOR.
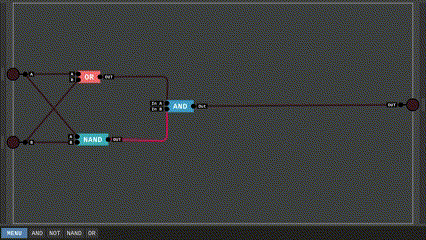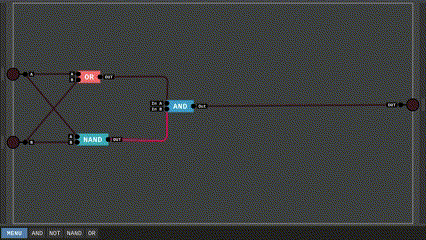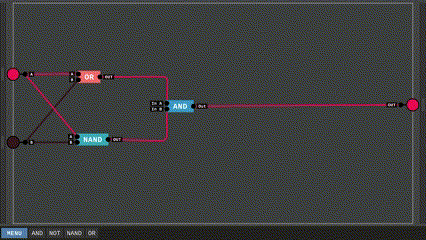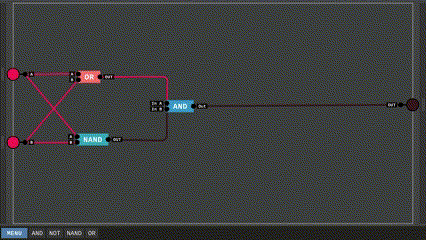
Bằng cách kết hợp giữa OR và NAND, ta tạo được một mạch XOR như trên. Bảng chân lý của nó như sau:
0 XOR 0 = 0
0 XOR 1 = 1
1 XOR 0 = 1
1 XOR 1 = 0
Đến đây ta đã có thể xây dựng nên mạch HALF-ADDER, đơn giản là dùng mạch AND cho đầu ra Carry và mạch XOR cho đầu ra Sum là xong.
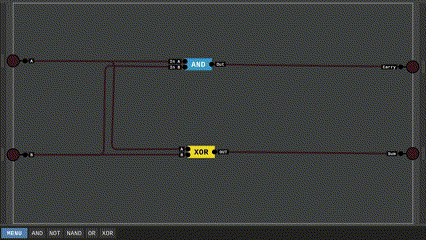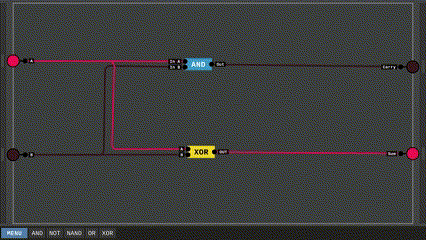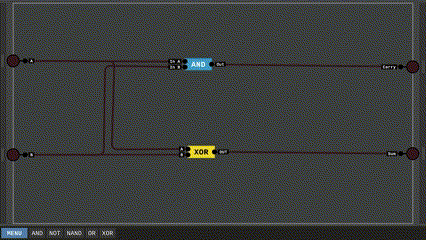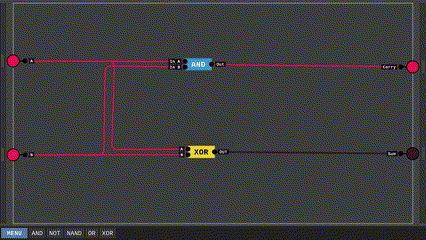
Sở dĩ gọi là HALF-ADDER là bởi vì mạch này chỉ cộng được 2 bit với nhau, nhưng trong bài toán cơ sở của chúng ta còn có phép cộng tới 3 bit. Hãy cùng xây dựng nốt phần còn lại. Ta có bảng chân lý của một mạch FULL-ADDER hay ngắn gọn là ADDER như sau:
| A (IN) | B (IN) | C (IN) | Sum (OUT) | Carry (OUT) |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
Nhờ mạch HALF-ADDER ta đã xây dựng trước đó, việc hoàn thành ADDER cũng khá dễ dàng. Ta lần lượt dùng hai mạch HALF-ADDER để cộng dồn kết quả cho Sum và dùng một mạch OR để lấy phần dư của một trong hai mạch HALF-ADDER là sẽ có được đầu ra Carry.
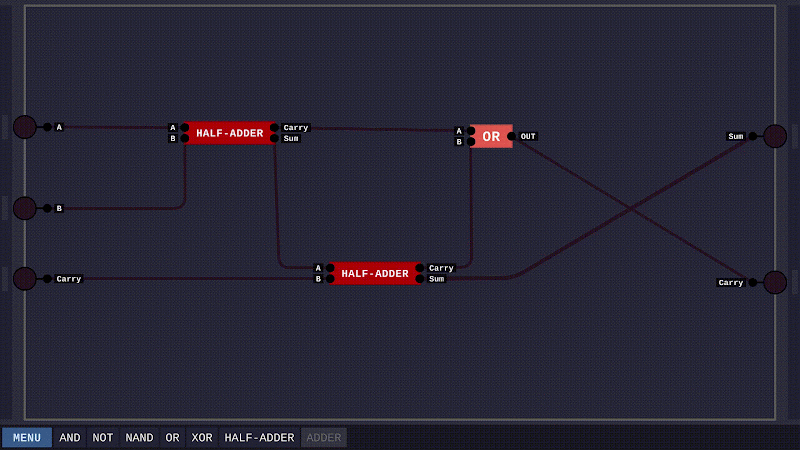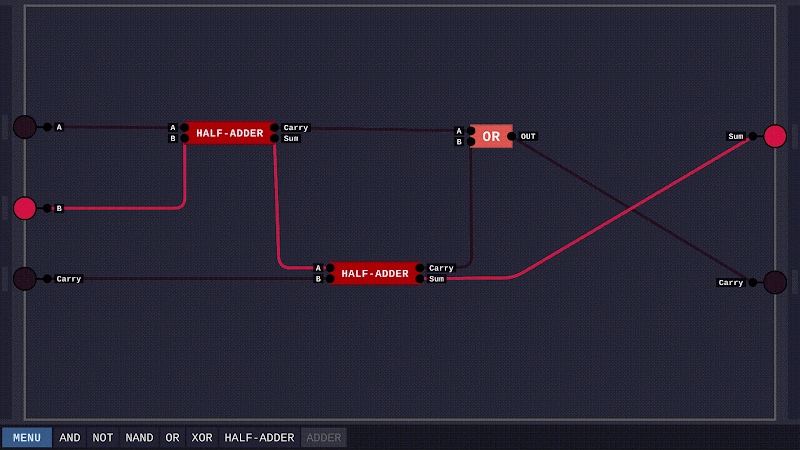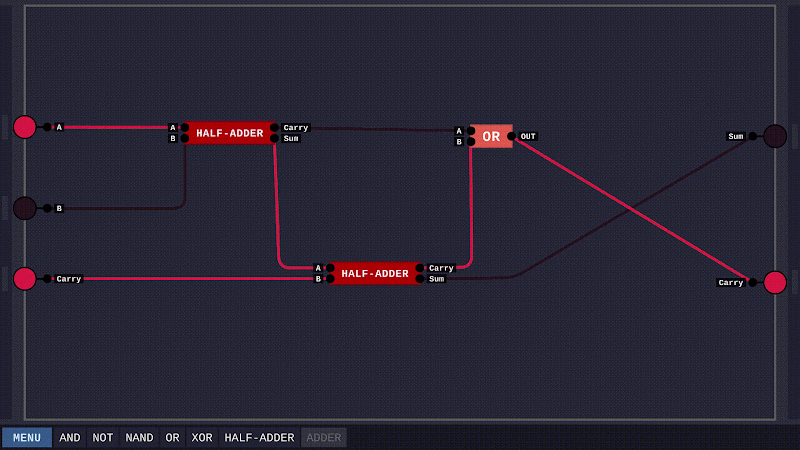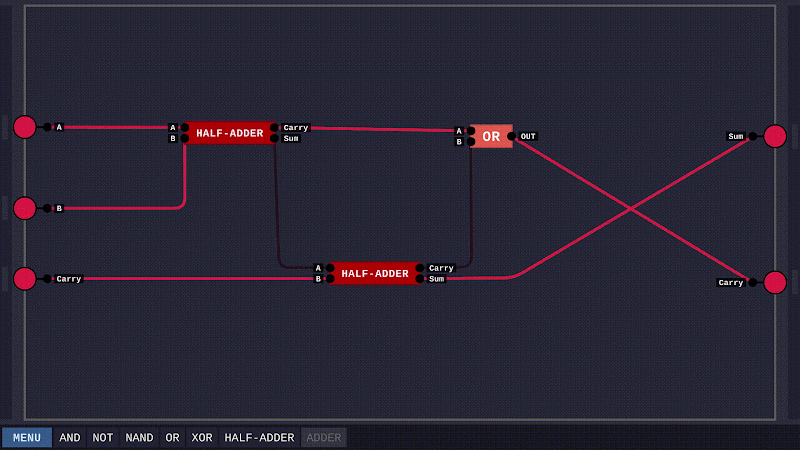
Như thế là ta đã hoàn thành bài toán cơ sở. Tiếp đó, để tăng tính thuyết phục, ta sẽ xây dựng một mạch cộng cho hai số nhị phân 4 bit.
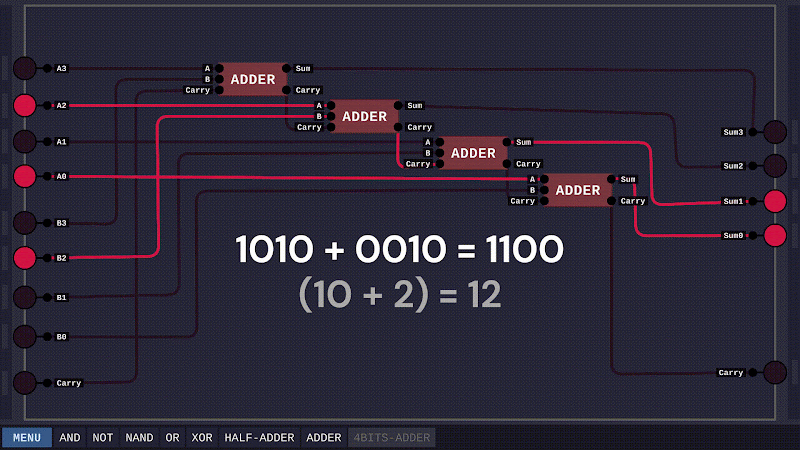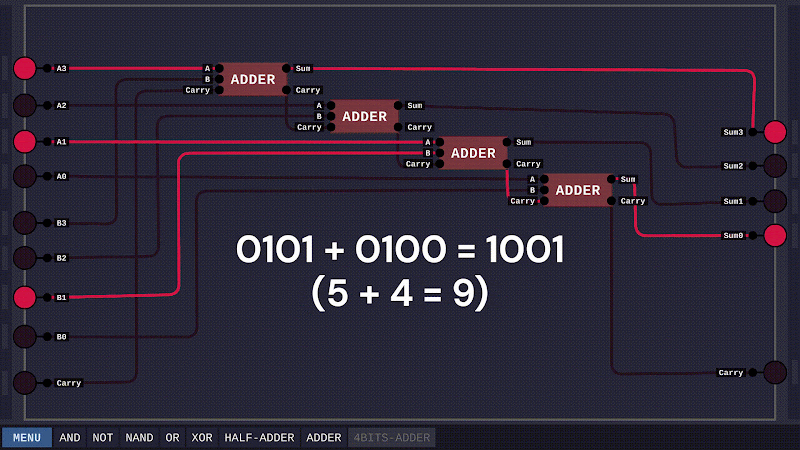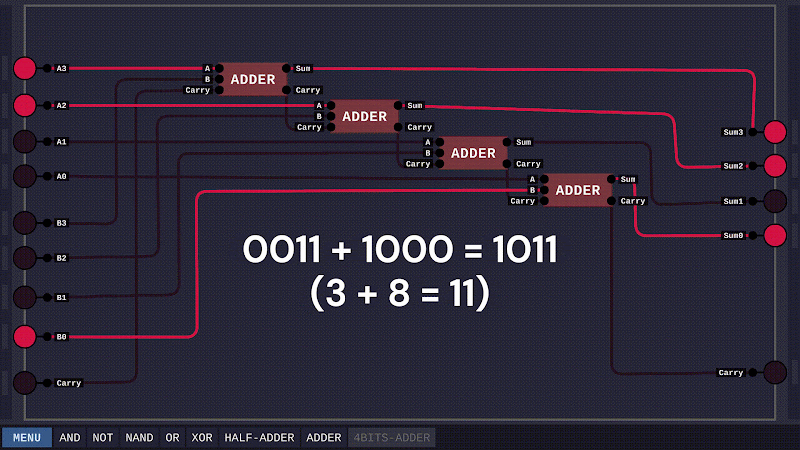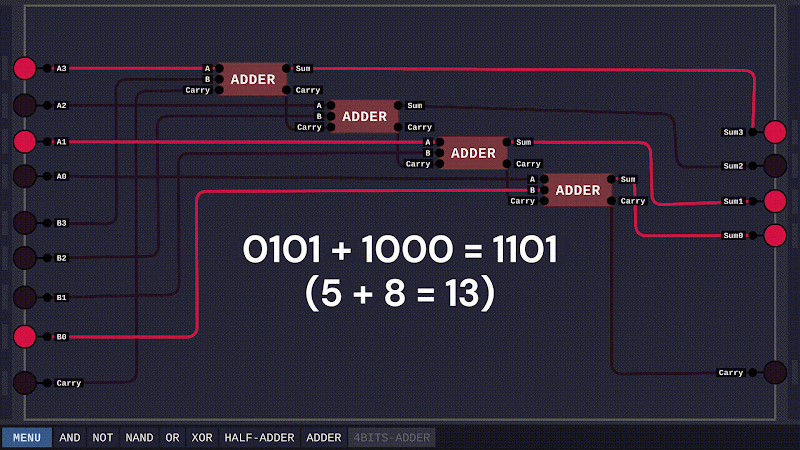
1,031 total views, 1 views today