Máy tính và hệ cơ số 2
Tác giả: Nguyễn Quỳnh Mai, Học viên khóa 2021-2024
Trong các hệ đếm thì hệ thập phân là thường gặp nhất, đây là hệ cơ số chúng ta thường dùng trong tính toán. Tiếp theo là hệ nhị phân cũng thấy nhiều vì đây là hệ cơ số máy tính sử dụng. Thế nhưng tại sao máy tính lại sử dụng hệ nhị phân và cách hoạt động của chúng như thế nào? Qua bài sharing này, mình sẽ chia sẻ với mọi người một vài điều cơ bản về mối quan hệ giữa hệ nhị phân và máy tính.
1. Tại sao máy tính sử dụng hệ đếm cơ số 2
Mỗi số trong máy tính là một tín hiệu điện, và trong những ngày đầu của máy tính, tín hiệu điện khó đo lường và kiểm soát rất chính xác. Sẽ có ý nghĩa hơn khi chỉ phân biệt giữa 2 trạng thái – được biểu thị bằng điện tích âm và điện tích dương. Vì vậy, các máy tính có kích thước phòng ban đầu đã sử dụng hệ nhị phân để xây dựng hệ thống của chúng và mặc dù chúng sử dụng phần cứng cũ hơn, cồng kềnh hơn nhiều, chúng vẫn giữ các nguyên tắc cơ bản. Các máy tính hiện đại sử dụng cái gọi là bóng bán dẫn để thực hiện tính toán với hệ nhị phân.
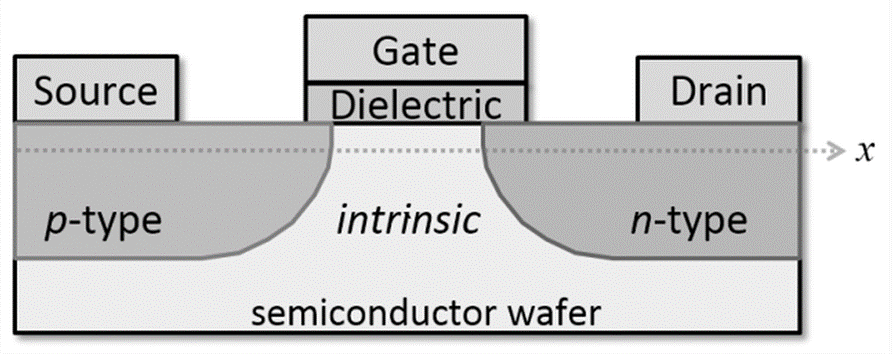
Về cơ bản, nó chỉ cho phép dòng điện chạy từ nguồn đến cống nếu có dòng điện trong cổng. Điều này tạo thành một chuyển đổi nhị phân. Các nhà sản xuất có thể chế tạo các bóng bán dẫn này cực kỳ nhỏ, đến tận 5 nanomet, hoặc có kích thước bằng hai sợi DNA. Đây là cách các CPU hiện đại hoạt động.
2. Máy tính có thể sử dụng các hệ cơ số khác không
Nhiều người sẽ nói rằng PC cũng quản lý dữ liệu trong hệ thập lục phân, nhưng thực ra, nó được sử dụng như một phương tiện biểu diễn các giá trị nhị phân để con người hiểu được: một giá trị vị trí duy nhất trong hệ thập lục phân đại diện cho bốn bit bộ nhớ, hai vị trí là tám bit hoặc một byte.
Hãy thử tưởng tượng một chiếc máy tính nào đó dựa trên hệ thập phân. Khi ấy sẽ có 10 trạng thái khả dĩ của dòng điện. Và mọi thứ sẽ được biểu diễn bởi những chữ số từ 0 đến 9. Điều này khó có thể xảy ra với cấu tạo của những máy tính ngày nay nhưng hoàn toàn có thể đối với những máy tính lượng tử.
Vậy hệ thống này có hiệu quả hơn hay không? Giả sử những công tắc của hệ máy tính nhị phân chiếm cùng 1 khoảng trống vật lý với những công tắc hệ đếm cơ số 10. Khi ấy những máy tính chạy hệ 10 này sẽ hoạt động với năng suất cao hơn là điều hiển nhiên. Vì thế mặc dù câu hỏi liệu rằng hệ nhị phân sẽ “không hiệu quả” là có vẻ đúng trong lý thuyết nhưng về mặt thực tế sử dụng ngày nay thì không.
Vấn đề ở đây là nếu bạn muốn sử dụng nhiều cấp điện áp, bạn cần một cách dễ dàng thực hiện các phép tính với chúng và phần cứng không thể thay thế cho điện toán nhị phân. Nó thực sự tồn tại; nó được gọi là máy tính thời gian, và nó đã xuất hiện từ những năm 1950, nhưng sự phát triển của nó dừng lại khá nhiều. Logic ternary hiệu quả hơn nhị phân, nhưng cho đến nay, không gì có sự thay thế hiệu quả cho bóng bán dẫn nhị phân, hay, không thể phát triển chúng ở cùng một quy mô nhỏ như nhị phân.
Lý do chúng ta không thể sử dụng logic ternary bắt nguồn từ cách các bóng bán dẫn được xếp chồng lên nhau trong một máy tính – thứ gọi là Cổng Gate.-và cách chúng được sử dụng để thực hiện toán học. Gates có hai đầu vào, thực hiện một thao tác trên chúng và trả về một đầu ra.
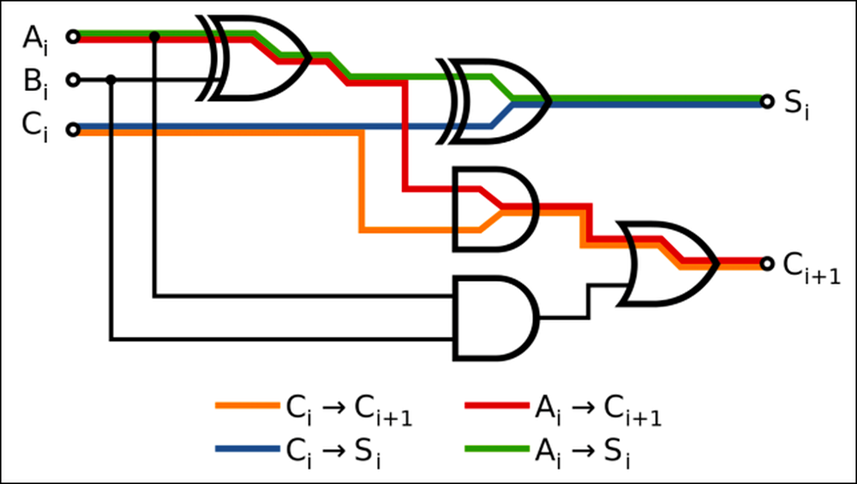
Điều này đưa chúng ta đến câu trả lời dài: toán học nhị phân là cách dễ dàng hơn cho máy tính hơn bất kỳ thứ gì khác. Boolean logic ánh xạ dễ dàng đến các hệ thống nhị phân, với True và false được biểu diễn bằng cách bật và tắt. Gates trong máy tính của bạn hoạt động dựa trên logic boolean: chúng lấy hai đầu vào và thực hiện một thao tác trên chúng như AND, OR, XOR, v.v. Hai đầu vào dễ quản lý. Nếu bạn đã vẽ biểu đồ các câu trả lời cho mỗi đầu vào có thể, bạn sẽ có cái được gọi là bảng chân lý:
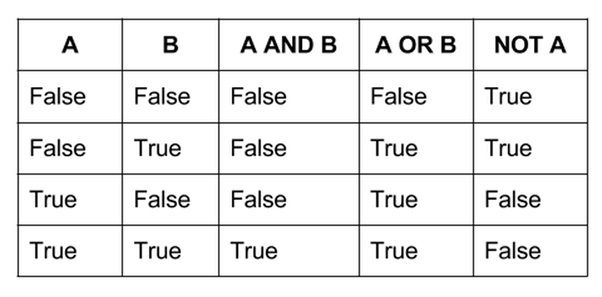
Một bảng chân lý nhị phân hoạt động trên logic boolean sẽ có bốn đầu ra có thể cho mỗi hoạt động cơ bản. Nhưng bởi vì các cổng ternary có ba đầu vào, một bảng chân lý sẽ có 9 hoặc nhiều hơn. Trong khi một hệ thống nhị phân có 16 toán tử có thể (2 ^ 2 ^ 2), thì một hệ thống ternary sẽ có 19.683 (3 ^ 3 ^ 3). Mở rộng quy mô trở thành một vấn đề bởi vì trong khi ternary hiệu quả hơn, nó cũng phức tạp hơn theo cấp số nhân.
Nói tóm lại thì ở thời điểm hiện tại, hệ đếm nhị phân là lựa chọn tốt nhất dành cho máy tính. Nhưng trong tương lai, cũng có thể sẽ có những chiếc máy tính mới, hiện đại hơn chạy trên những hệ đếm khác.
3. Một số phép toán cơ bản trên hệ cơ số 2
Ta đã biết máy tính thực hiện các phép toán trên hệ nhị phân, vậy các phép toán ấy được thực hiện như thế nào?
3.1. Phép chuyển đổi hệ cơ số
Máy tính biểu diễn kết quả của các phép toán đa số trên hệ cơ số 10, vậy nên máy tính cần liên tục chuyển đổi giữa hệ cơ số 2 và 10. Và đây là cách máy tính làm điều
đó:
a. Chuyển đổi hệ cơ số 10 sang hệ cơ số 2
Gồm 2 bước:
- Chia lặp đi lặp lại số đó cho 2. Phép chia dừng lại khi kết quả lần chia cuối cùng bằng 0.
- Lấy các số dư theo chiều đảo ngược sẽ được số nhị phân cần tìm.
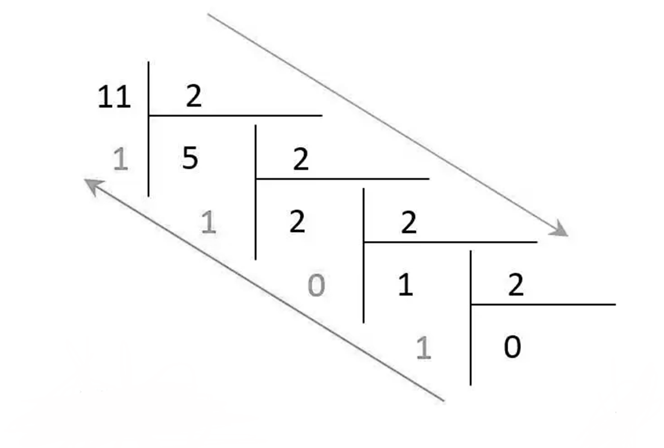
b. Chuyển đổi hệ cơ số 2 sang hệ cơ số 10
Cách chuyển đổi này được biểu diễn theo công thức tổng quát, với r = 2 và n là số chữ số của một số:
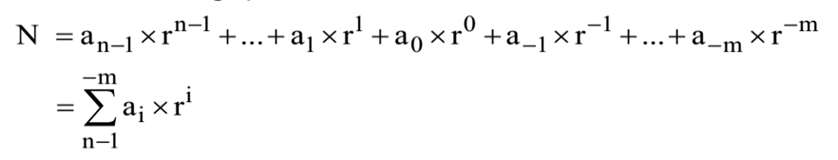
3.2. Các phép toán logic
Ta có 4 phép toán logic: and, or, xor và not, được biểu diễn theo bảng sau:
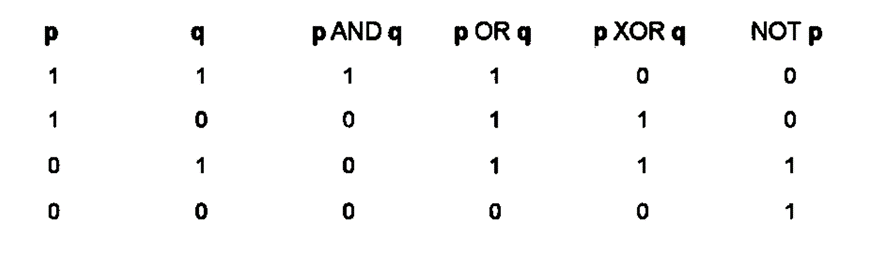
Và cách tính toán cho một dãy bit cũng tương tự. Ví dụ với phép toán A or B:
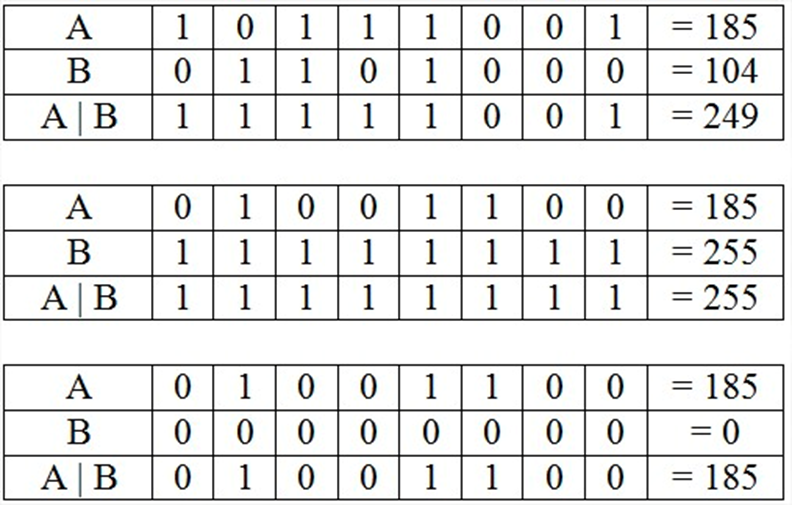
3.3. Các phép toán cộng trừ nhân chia
Để cộng hai đơn vị trong hệ nhị phân thực hiện theo nguyến tắc sau:

Ví dụ: Cộng hai số 1000111_210001112 và số 11110_2111102
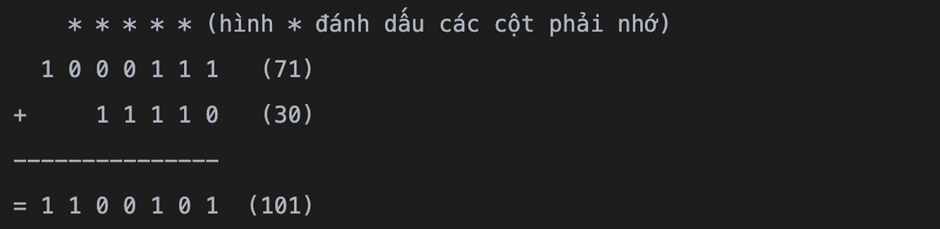
(Tương tự với phép trừ)
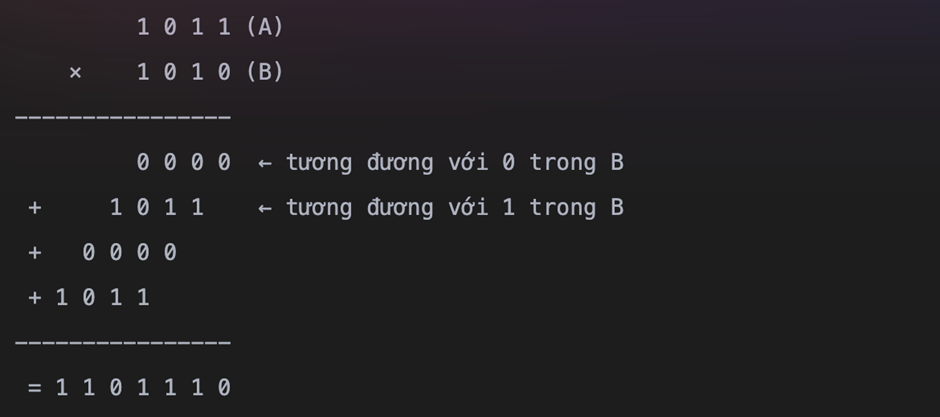
Phép tính nhân trong hệ nhị phân cũng tương tự như phương pháp làm trong hệ thập phân. Hai số AA và BB được nhân với nhau bởi những tích số cục bộ: với mỗi con số ở BB, tích của nó với số một con số trong AA được tính và viết xuống một hàng mới, mỗi hàng mới phải chuyển dịch vị trí sang bên trái, hầu cho con số cuối cùng ở bên phải đứng cùng cột với vị trí của con số ở trong BB đang dùng. Tổng của các tích cục bộ này cho ta kết quả tích số cuối cùng.
Vì chỉ có hai con số trong hệ nhị phân, nên chỉ có 2 kết quả khả quan trong tích cục bộ:
- Nếu con số trong BB là 00, tích cục bộ sẽ là 00
- Nếu con số trong BB là 11, tích cục bộ sẽ là số ở trong AA.
Ví dụ: hai số nhị phân 1011_210112 và 1010_210102 được nhân với nhau như sau:
Phép chia nhị phân cũng tương tự như phép chia trong hệ thập phân. Ví dụ:

Bài chia sẻ của Mai đến đây là hết. Cảm ơn mọi người đã đọc bài!
6,859 total views, 5 views today